1 33 honeycomb
| 133 honeycomb | |
|---|---|
| (no image) | |
| Type | Uniform tessellation |
| Schläfli symbol | {3,33,3} |
| Coxeter symbol | 133 |
| Coxeter-Dynkin diagram | |
| 7-face type | 132 |
| 6-face types | 122 131 |
| 5-face types | 121 {34} |
| 4-face type | 111 {33} |
| Cell type | 101 |
| Face type | {3} |
| Cell figure | Square |
| Face figure | Triangular duoprism |
| Edge figure | Tetrahedral duoprism |
| Vertex figure | Trirectified 7-simplex |
| Coxeter group | 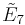 , [33,3,1] , [33,3,1] |
| Properties | vertex-transitive, facet-transitive |
In 7-dimensional geometry, 133 is a uniform honeycomb, also given by Schlafli symbol {31,3,3}, is composed of 132 facets.
Contents |
Construction
It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 7-dimensional space.
The facet information can be extracted from its Coxeter-Dynkin diagram.
Removing a node on the end of one of the 3-length branch leaves the 132, its only facet type.
The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the trirectified 7-simplex, 033.
The edge figure is determined by removing the ringed nodes of the vertex figure and ringing the neighboring node. This makes the tetrahedral duoprism, {3,3}×{3,3}.
The face figure is determined by removing the ringed nodes of the edge figure and ringing the neighboring node. This makes the triangular duoprism, {3}×{3}.
Kissing number
Each vertex of this polytope corresponds to the center of a 6-sphere in a moderately dense sphere packing, in which each sphere is tangent to 70 others; the best known for 7 dimensions (the kissing number) is 126.
Geometric folding
The 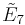 group is related to the
group is related to the 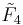 by a geometric folding, so this honeycomb can be projected into the 4-dimensional demitesseractic honeycomb.
by a geometric folding, so this honeycomb can be projected into the 4-dimensional demitesseractic honeycomb.
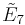 |
 |
|---|---|
| {3,33,3} | {3,3,4,3} |
See also
References
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]